SHCTF2024 Crypto WriteUp
SHCTF2024 Crypto WriteUp
Author: dawn1ight
这里记录一下一些值得学习的题目
有些是板子题,也记录一下,现在年纪大了健忘😅
Challenges: https://shc.tf/
References:
- SHCTF2024-week1-crypto&其他 - Naby - 博客园
- SHCTF-2024-Week2 官方WP
- SHCTF2024-week3-Crypto - Naby - 博客园
- SHCTF-2024-Week3 官方WP
- 2024-SHCTF-week4-wp-crypto | 糖醋小鸡块的blog
- SHCTF-2024-Week4 官方WP
[Week1] baby_mod
from Crypto.Util.number import * |
看到题目打算直接爆破tmp解方程组的
发现题目没有给n
这里的r和t都大于p q,所以相互取模得
\begin{gather*} leak \mod r = p*r-q*t-tmp \mod r \\ leak + tmp \mod r = -q*t \mod r \\ q = (leak + tmp) * (-t)^{-1} \mod r \end{gather*}
同理:
exp : SHCTF2024-week1-crypto&其他 - Naby - 博客园 (cnblogs.com)
from Crypto.Util.number import * |
[Week1] d_known
from Crypto.Util.number import * |
第一次看到已知e c d,未知n的,顺手记录一下
因为 $$e∗d=1+k(p-1)∗(q-1)$$
其中e.bit_length = 17 , d.bit_length = 2044,e*d.bit_length = 17+2044=2061
所以k.bit_length = 2061-2048 = 13
k的位数较小,直接爆破,得到k后,开根找p q
exp: SHCTF2024-week1-crypto&其他 - Naby - 博客园 (cnblogs.com)
from Crypto.Util.number import * |
[Week2] worde很大
import gmpy2 |
第一眼看:dp泄露,直接上脚本
import gmpy2 as gp |
代码跑起来发现问题:e太大了,for x in range(1, e):循环不了
这里复习一下dp泄露的推导:RSA | Lazzaro
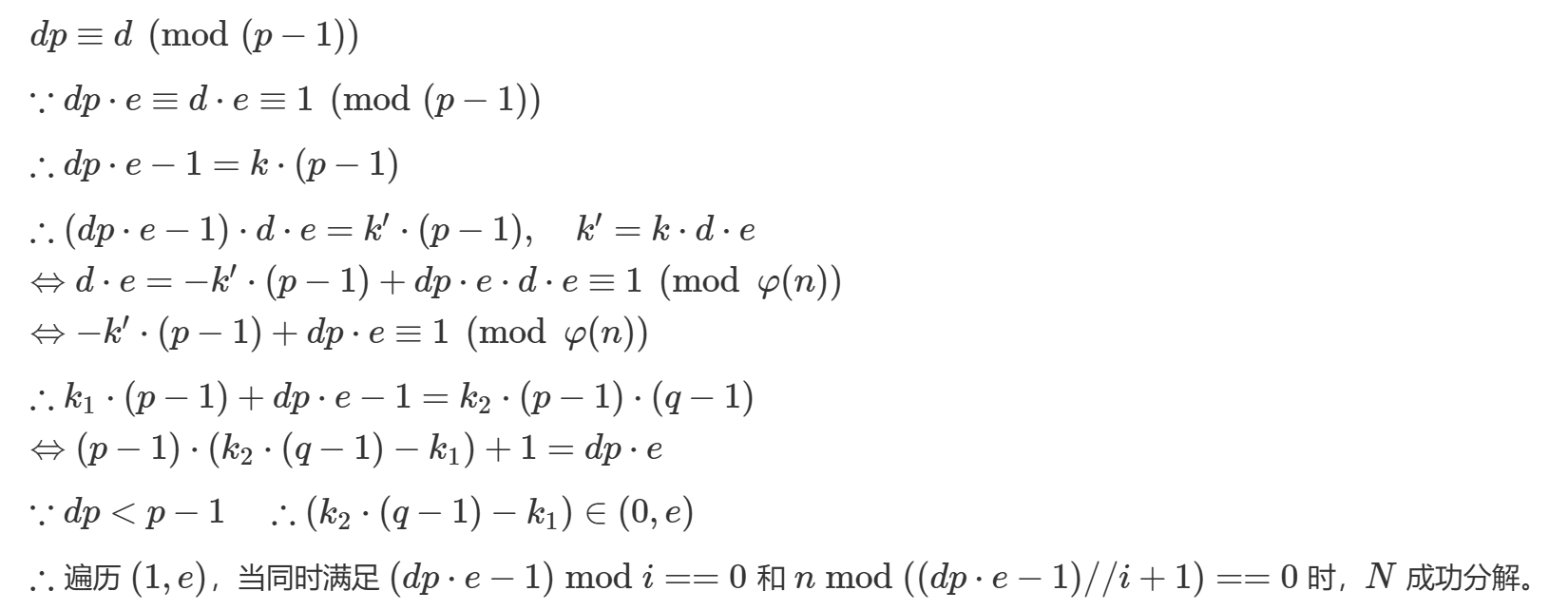
[官方WP](SHCTF-2024-Week2 官方WP)中给出了另一种思路:
\begin{array} \\ d_p \equiv d \mod (p-1) \\ ed \equiv 1 \mod (p-1)(q-1) \\ m^{ed_p}\mod n \equiv m^{ed\mod (p-1)} \mod p \equiv m^{1+k(p-1)}\mod p \\ Fermat's\;little\;theorem: a^{p-1} \equiv 1 \mod p \\ \therefore m^{1+k(p-1)}\mod p \equiv m \mod p \\ \therefore m^{ed_p}\mod n - m \equiv 0 \mod p \\ p = gcd(m^{ed_p}\mod n - m , n) \end{array}
import gmpy2 |
[Week2] pading
from Crypto.Util.number import * |
在小e下,知道m的低位
这种知道高低位的基本都是coppersmith的应用
import libnum |
参数的考虑:
pad我们是知道的,且告诉了我们flag的位数为39,39 * 8 = 312,e次方为312* 3 = 936,
而n的位数为1024,312的flag相对于1024的n来说是小值,可用coppersmith的方法求得,
beta的值依据912/1024=0.91取整为0.9,epslilon的值慢慢放小
[Week2] E&R
#sage |
复习一下RSA剪枝
from Crypto.Util.number import * |
ECC部分,因为n不是质数,E = EllipticCurve(Zmod(n),[114514,1919810])无法直接算E.order
第二部分是ECC,曲线在模n上的阶不好直接算,而
n = pq,那么我们可以分别构建在模p和模q上的曲线,然后分别计算其阶,进而得到曲线在模n上的阶,接下来就计算出e对于曲线的逆元求出点G,其横坐标即为flag部分
#sage |
[Week3] Approximate_n
from Crypto.Util.number import * |
AGCD问题(The Approximate Common Divisor Problem, 近似最大公约数问题)
第一部分中返回了三个AGCD值,此时我们可以考虑使用传统的AGCD问题中的SDA丢番图格进行攻击
from Crypto.Util.number import long_to_bytes |
第二部分知道N2和N2_reveal的值,PACD问题。通过论文 Passive SSH Key Compromise via Lattices,我们可以知道PACD问题的解决手段,选取参数
格:
\begin{array} \\B= \begin{pmatrix} -2^{2log_r} & 2^{log_r}N_1 & 0\\ 0 & -2^{log_r} & N_1\\ 0 & 0 & N_0 \end{pmatrix}\\ \end{array}
B.LLL()得到
from Crypto.Util.number import * |
还有另一种
from tqdm import * |
[Week3] babyLCG
from Crypto.Util.number import * |
复习一下LCG:
seed>>80有位移,应该要用格
第一种:手动构造格 SHCTF2024-week3-Crypto - Naby - 博客园
from Crypto.Util.number import long_to_bytes |
第二种:上二元coppersmith 记 LCG 例题-CSDN博客
已知的高320bit
将高320bit和低80bit分别记为和
\begin{array} \\ C_2=H_2+L_2 \\ C_1=H_1+L_1 \\ C_2=a\times C_2+b \mod p \\ H_2+L_2=a\times (H_1+L_1)+b \mod p \\ f = a\times (H_1+L_1)+b-(H_2+L_2) \\ L_1,L_2\,small,\;\mod p\;copper \\ \because C_1=a\times seed+b \mod p \\ \therefore (C_1-b)\times a^{-1}\mod p \end{array}
# sage |
[Week3] Shamir
from Crypto.Util.number import getPrime,bytes_to_long |
Shamir门限,多项式最大系数为100,通过交互得到101个点的坐标,利用拉格朗日插值法得到这100个系数的值
from pwn import * |
另外也可以用sagemath自带的朗格朗日插值函数
from pwn import * |
[Week3] 大学×高中√
from Crypto.Util.number import * |
题目改编自 第二届黄河流域网络安全技能挑战赛 | DexterJie’Blog
那个是这个是,也是构造格(week3的题目怎么全是格……)
格子如下:
\begin{array} \\ m = arccos(leak)+2k\pi \\ L = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & arccos(leak)\\ 0 & 0 & 2\pi \end{pmatrix}\\ (m,-1,-k)L=(m,-1,0)\\ leveling: L= \begin{pmatrix} 1 & 0 & 2^{750}\\ 0 & 2^{375} & arccos(leak)\times2^{750}\\ 0 & 0 & 2\pi\times2^{750} \end{pmatrix}\\ (m,-1,-k)L=(m,-2^{375},0) \end{array}
这里学习一下格的配平:crypto-格密码实战入门(svp问题)
Hermite定理:这个定理给出了最短向量的上界
对于n维的格L,都有一个非零向量v属于L,满足:
表示格基的数量积,n为维度,为格L(矩阵)的行列式
以这个题目为例: ,,
题目中给出len(flag)==47,bit_length(m)配平后
from Crypto.Util.number import * |
[Week3] baby_lock
class Random(object): |
Xorshift128Plus伪随机数算法 随机数之 xorShift128Plus 板子 - deaf - 博客园
本题有一点改动
这个漏洞在v8的
Math.random()中被发现(已修复)只需要3个连续state,Z3求解即可
JavaScript中Math.random函数的伪随机性解析以及破解方法研究
# sage |
[Week4] MT19937
import hashlib |
[1212937457, 714280275, 2934808054, 289447810, 634020656, 2582053193, 2648476152, 3584472561, 2877037797, 1051288028, 3007240724, 3583122714, 2377373219, 2233668169, 2300136290, 4277363949, 572508719, 3707687803, 868724505, 2234515288, 2182162330, 2354654192, 3676064525, 16386761, 1934246009, 396534601, 3406538372, 1978740790, 51554945, 1642830773, 3255471879, 249329746, 1871028531, 1670146144, 3955249559, 3523216280, 4225679888, 1979625069, 1711120506, 4224015378, 2357192253, 1437719734, 1861766583, 252037050, 3805173581, 3845899039, 239338040, 3335618070, 1909354144, 2380236080, 3120658839, 2738735651, 1749563272, 4028406006, 198730175, 4095736523, 2224365497, 1850797931, 123559677, 277130374, 1547602417, 2312967225, 1064405558, 620877831, 4182002366, 2717144120, 2424475877, 1261886189, 2666842961, 1250633055, 1445939400, 2496676732, 46718503, 1726056600, 2892333819, 3874613567, 2801764620, 3279121957, 62950328, 14090298, 3016963976, 235881318, 1152787765, 3549713637, 3184265794, 461262349, 1835258817, 706701716, 366259495, 2484440259, 2306336615, 2418024433, 107268664, 3018120752, 3915797798, 1685880034, 2782876985, 2876720582, 3803172243, 1745503879, 1965535595, 2831775453, 3139448870, 770826076, 559187920, 4292272948, 86904027, 1821662944, 58381562, 250790584, 2122997254, 2937312684, 3225034461, 1493971528, 913420791, 2911905254, 2938402784, 1430747115, 2654595902, 3315197237, 602765188, 1471009311, 3788529131, 913593424, 3280524381, 1554400422, 3250536147, 3480550436, 821401975, 3216026683, 762420368, 1733854366, 2395038075, 533527872, 3040490234, 2855012365, 2984904790, 2830464734, 2200935030, 523059886, 3795772367, 2905400361, 667720140, 3155311553, 1860651089, 1053555607, 2889478721, 1812821011, 3391980212, 3433665687, 2480476597, 1319654037, 1076583906, 2287201297, 966928688, 2542225146, 2246098689, 3117124345, 1844896511, 3104215564, 1303510082, 2924158615, 3648677443, 3308489255, 3809196505, 3199516268, 2254502655, 2126047470, 1763846642, 3851973930, 1280609700, 2415985988, 1312349771, 2103486452, 4229394974, 1937464844, 2763672456, 1366425769, 1532462738, 1864298394, 1203192658, 3679892306, 4138733297, 39437090, 1317880030, 132948638, 2315846286, 3394291148, 3207221552, 3834885856, 2367158425, 3183864791, 3303289072, 519407526, 4127464161, 1556426685, 2427155757, 2010011401, 2823249259, 3638339516, 2266010959, 345885116, 471672470, 2713191580, 731238671, 1694687550, 2523761501, 3533913138, 163820753, 1829608711, 587056408, 1129980234, 3642159144, 2546599527, 758703728, 1713442774, 1864598338, 2763096157, 2308766766, 1132350895, 2776604596, 1921085522, 1409581297, 2643399928, 3285649744, 1248611904, 2694186262, 2676127368, 2579578748, 3784393865, 2655293049, 1378866508, 1251610536, 1048557165, 3045231444, 4236456301, 2496231577, 4118010676, 3079411364, 2425576144, 2431718306, 543894373, 118186072, 2594647421, 1833894329, 3876640493, 1916631983, 2765860034, 3905895682, 2207230275, 2554838603, 3199831939, 2516271151, 3080023814, 3594335532, 1197450849, 2621744299, 447615180, 1616950869, 3109651542, 2553431350, 4165466937, 2130063794, 1459492895, 1141470511, 948009682, 325807524, 1681494454, 3137320840, 4219461371, 609761579, 942363481, 2404858793, 1697226342, 830264373, 230968933, 831865647, 4164463522, 2968510743, 1464271639, 1397831008, 2559413030, 3515044508, 772056268, 3152446673, 3117754594, 833212973, 4252629747, 2565179775, 3005093783, 3595030314, 4042182692, 298671165, 3183128227, 3429794312, 4122368172, 1900961662, 3589294443, 3190786481, 1744404482, 1921785452, 3011999869, 642164068, 3695788414, 2275346981, 1428956574, 2697326707, 2202213004, 3287889517, 919861723, 726410498, 337174656, 2417998504, 2752587611, 3856581958, 141509063, 1762431188, 2065705145, 2031960873, 1892209091, 2395039500, 1058479586, 1537034270, 502217054, 3102018820, 1433274316, 1372952271, 2918921770, 239909451, 1398298200, 2339489735, 372558373, 2263872236, 2426192905, 337209508, 3983991978, 2574803724, 2837664572, 1569892789, 2625063195, 3262762020, 24150029, 2016099290, 2239153990, 85602273, 973040529, 2956276779, 4218049523, 2043716624, 2788573458, 1218787308, 939708241, 2861205992, 2427634523, 4128874493, 2326852266, 2593724377, 1680473968, 2763572707, 4240616686, 2863701585, 3551633590, 1765256405, 2110583291, 357590304, 2511138801, 859903599, 35591840, 3786321031, 3559501147, 3107666783, 2356867678, 1369801910, 2488594855, 2148205170, 3944224524, 2219844222, 466009157, 2328231114, 2777059464, 1585865212, 2871297568, 2558165993, 1561563095, 438633926, 2619385032, 2185942244, 2501145168, 2161107203, 912485991, 3956413626, 4065963551, 1527306118, 378382496, 1016367697, 82832444, 2484726280, 867566307, 1037338825, 4291735272, 901722138, 3956112428, 1060890097, 4210262544, 2525835262, 786274933, 2563584713, 2738164238, 3438656534, 564065202, 3288501195, 1074332184, 2947775555, 3790174897, 3607901153, 2332098514, 3648669449, 3879104921, 3983960923, 548882335, 1817587379, 1555057777, 2705918139, 2755720626, 2706833366, 2947946695, 3082750952, 2323554320, 1804494628, 1677086381, 2771841028, 2470056271, 3431120732, 4073503495, 2929631518, 80800254, 605951710, 1664206366, 2498279527, 360922649, 2590660538, 3724444465, 3559953317, 3002864163, 3369368155, 1569518356, 3831143803, 4184782515, 1602338537, 2640186368, 2864951447, 514648741, 887020932, 166121609, 476244781, 2238614863, 3039706334, 3586500526, 3038068930, 3989751746, 3699955508, 3559348520, 884358906, 444882591, 3769021913, 3665754928, 1911261614, 1234192084, 3450557803, 3232410240, 494096069, 660552292, 1365481833, 520081058, 1027987838, 3165505556, 1257833693, 2146291679, 3634622224, 589123893, 1195030125, 1602406253, 772753497, 2661121530, 2938530200, 1070706826, 3890477657, 2112901265, 4253917692, 2291562806, 67613984, 2608069358, 1726139310, 3018885048, 367067728, 3838771641, 1357927847, 2616452172, 722979624, 4153031784, 607660099, 3164865398, 3199368055, 1885230388, 1055777913, 3475913336, 1546318749, 578282810, 1558944130, 2955660875, 2214838829, 4202836988, 1405916968, 2593459723, 3648360966, 3644813488, 598912719, 876098814, 355483438, 685352898, 4099087273, 2983380912, 450980374, 2753208777, 429297943, 3462109454, 3134522829, 2064548393, 2200750558, 4247753845, 251220053, 1556849099, 2022648175, 3563632884, 2175932589, 1463719656, 1887673611, 3541708446, 3033219582, 3255799816, 534398633, 3481196045, 825005812, 1629237540, 640085217, 899503755, 3105157116, 488231507, 2708835929, 2648663900, 2048030022, 1503411342, 4059850866, 1281156549, 3171426598, 2637361895, 1110841056, 606897504, 3001264062, 912267483, 148124465, 202684836, 1425732680, 3637635336, 1455737055, 2977077407, 54987379, 1056796337, 1832170261, 1870208138, 4074249428, 2993704297, 381772606, 2362720677, 2164369676, 250156737, 3409786877, 1590821450, 2959971180, 3682255149, 302283211, 4204651015, 1294232346, 3088162584, 4209012441, 784333825, 1275400791, 885466807, 1249631254, 1236809354, 2627231325, 2391839654, 1638467843, 2797229961, 3799496431, 237846505, 3432655604, 1690038717, 1493561006, 4229115929, 3784624191, 2891696687, 3557702324, 1120718375, 2593253432, 1415584860, 551110044, 1510986691, 3267929936, 2341598281, 247215742, 3192053018, 2856032615, 3290505354, 907961089, 4128700570, 4195745607, 2035634741, 1047086449, 216435127, 1997121891, 3391563810, 2813128796, 1517545322] |
Python的random库用的MT19937伪随机数算法,生成范围在 的均匀分布的32位整数,该算法的周期为,故名为 MT19937
MT19937算法实现:
def _int32(x): |
需要已知624个32bit的数来预测输出,flag1符合情况
可以用randcrack库或extend_mt19937_predictor库来解决
import hashlib |
import hashlib |
但flag2部分只给出了600个随机数,无法直接预测。
MT19937在前624个随机数生成完毕之后,整个state会做一次twist,twist代码:
def twist(self): |
state经过twist后,其第i个位置其实也只与原来state的三个位置有关,分别是:
由于对于m2来讲,我们只需要预测twist过后的前156个数,所以只要有397+156=553个数字就足够了。而我们拥有前600个随机数,也就拥有state的前600个位置,绰绰有余。
而最简单的实现依然是用randcrack,由于它要求提交满624个32bit的数字才能预测,所以553-624之间的数字可以随便提交一些,不会影响加密m2的key值。
from randcrack import RandCrack |
[Week4] babyHash1
from Crypto.Cipher import AES |
from Crypto.Cipher import AES |
[Week4] babyHash2
FLAG = "SHCTF{XXX_FAKE_FLAG_XXX}" |
from Crypto.Util.number import * |
[Week4] siDH
#!/usr/bin/env sage |
P1=(3722377589495565619388409947786216655637784681305941494147641084588810631146007176891913880271007127410796381111369183814847421656105900790804342643108*x + 8802687499644901060050022727432797409089156524380319488542634490587555795650045132570968389279817924873049502727897060507742746276768059101617693509917 , 3719477936206364187390068985145413157800621156741491559595580900652585286439418248577575633342364501408686579893456793185782751143171546872666909621050*x + 11747436493943707843147767337329761069262174137296210697323632536020627422974942280457502098526627796314363833333722260721915312017545212458579310144482) |
又学到了,这个是SIDH(超奇异同源Diffie-Hellman秘钥交换算法),一种后量子安全秘钥交换协议
Castryck-Decru攻击是一种针对Supersingular Isogeny Diffie-Hellman (SIDH)协议的密钥恢复攻击。该攻击由Wouter Castryck和Thomas Decru于2022年提出,旨在利用椭圆曲线上的扭点信息和秘密同态的度数来计算所需的同态。攻击的核心在于利用椭圆曲线上的小非标量自同态的存在性,从而在多项式时间内恢复出用于生成秘密同态的整数。
论文原文: 975.pdf
其中在EB1最后面找到
p = 13175843156907117380839252916199345042492186767578363998445663477035843932020761233518914911546024351608607150390087656982982306331019593961154237431807 |
分解找到,
\begin{array} \\ a_1 = 250 \\ b_1 = 159 \\ a_2 = 486 \\ b_2 = 301 \end{array}
构造椭圆曲线,后面有点超模了
官方wp下来了
(sage-build)$ sage sol1.sage --parallel |
import public_values_aux |
(sage-build)$ sage sol2.sage --parallel --sandwich |
import public_values_aux |
$ python sol3.py |
from Crypto.Util.number import * |
[Week4] baby_rsa
#https://github.com/jvdsn/crypto-attacks |
论文题 34940373.pdf
今年高校密码挑战赛也出了 2024-高校密码挑战赛赛题一-wp-crypto | 糖醋小鸡块的blog
这里题目没给出d的位数,bitlen(d)猜测512位
from Crypto.Util.number import * |







